http://www.stat.ufl.edu/~athienit/Tables/Ztable.pdf
the table tells you the area to the left of the z-score in the table.
the z-score is a two decimal z-score.
the integer digit and the first decimal place digit are under the column heading of z.
the second decimal place digit is under the column heading of what it is.
for example:
z-score of -1.34 would find -1.3 under the z column heading and .04 under the .04 column heading.
the z-score combines -1.3 and .04 to get -1.34.
the table only shows the area under the normal distribution score to the left of the indicated z-score.
if you want the area to the right of the z-score, you have to subtract the area to the left of the z-score from 1 and you will get the area to the right of the z-score.
for example:
area to the left of z-score -1.34 is equal to .0901 and area to the right of z-score -1.34 is equal to 1 minus .0901 = .9099
if you are looking for the area between two z-cores, then you find the area to the left of both z-scores and you subtract the smaller area from the larger area.
for example, area between -.34 and .62 would be found as follows:
area to the left of -.34 = .3669
area to the left of .62 = .7324
area between -.34 and .62 = .3655
if you use this table, you should get:
area: equals a) to the left of z= .94 .8264 b) to the right of z=-0.65 1 - .7422 = .2578 c) to the right of z=1.76 1 - .9608 = .0392 d) between z=-0.34 and 0.62 .7324 - .3669 = .3655
bear in mind that the z-scores in the table are rounded to two decimal digits and the area to the left of those z-scores are rounded to 4 decimal digits.
this leads to small errors that usually don't mean too much.
if you need greater accuracy, then a scientific calculator like the ti-84 plus and ti-83 plus can give you many more digits of accuracy.
a good online calculator that shows you visually what happens can be found at the link.
http://davidmlane.com/hyperstat/z_table.html
http://davidmlane.com/hyperstat/z_table.html
your inputs to and outputs from this calculator would look like this:
you don't need to, but for clarity of reference, you can clear the built in entries before using the calculator.
it makes your selections stand out better.
you need to select the option that suits what you're looking for and then hit the return or select recalculate.
the answer is on the bottom.
here's what your problem inputs and outputs look like in turn.
problems in turn are:
a) to the left of z= .94
b) to the right of z=-0.65
c) to the right of z=1.76
d) between z=-0.34 and 0.62
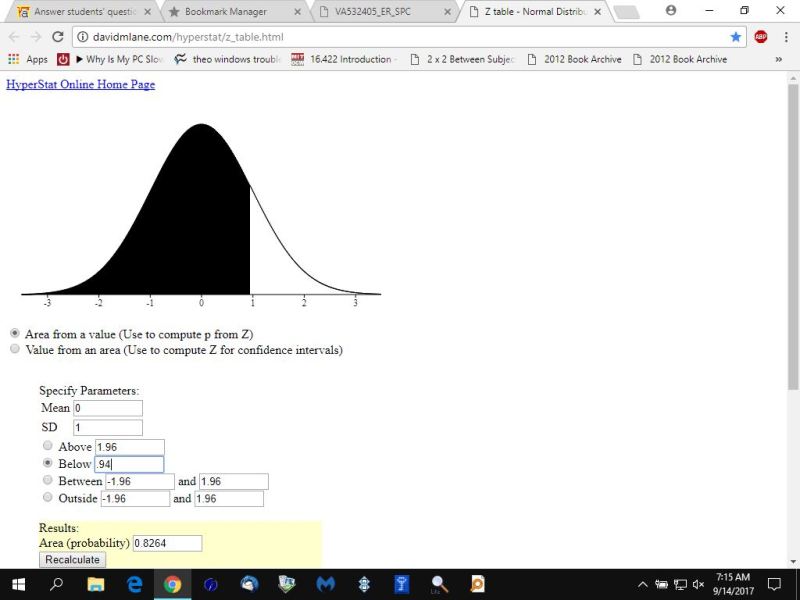



you will notice that the tables yielded .3655 in the last problem while the calculator yielded .3654.
this is due to using rounded numbers for intermediate results in the table versus only rounding at the end when using the calculator.