Question 1092284: The time is past 2 o'clock. In 10 minutes, the minute hand will be as much ahead of the hour hand as it is now behind it. What time is it?
Found 2 solutions by greenestamps, ikleyn:
Answer by greenestamps(13203)   (Show Source):
You can put this solution on YOUR website!
From the given information, we know, since the hour and minute hands move at uniform rates, that the minute hand and hour hand will be pointing in exactly the same direction 5 minutes from now.
The minute hand makes 12 revolutions every 12 hours; the hour hand makes 1. That means the minute and hour hands are pointing in the same direction 11 times every 12 hours. Again since the hands both move at uniform rates, we know the interval between times when the hands point in the same direction is 12/11 hours.
The minute and hour hands point in the same direction at 12:00. So the time shortly after 2:00 when the hands align will be 24/11 hours after 12:00, or 2/11 hours after 2.
2/11 hours = 120/11 minutes = 10 10/11 minutes.
10/11 minutes = 600/11 seconds = 54 6/11 seconds.
To the nearest second, the time shortly after 2 when the hands align is 2:10:55.
So the current time is 5 minutes before that -- at 2:05:55.
Answer by ikleyn(52814)  (Show Source):
You can put this solution on YOUR website! .
The way to solve this problem is to write equation for angles that the minute hand and the hour hand make with . . . let say,
with the vertical direction, with the direction "vertically up".
So, we will count angles clockwise starting from that direction "vertically up".
The minute hand makes one full revolution in 1 hour = 60 minutes. Hence, its angular velocity is 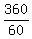 = 6 degrees per minute.
The hour hand makes one full revolution in 12 hours. Hence, its angular velocity is 12 times less, i.e.  =  degrees per minute.
Let "t" be the number of minutes after 2:00 pm which is under the question.
Now the minute hand is in position 6t degrees, while the hour hand is in position  degrees.
Thus the angle between the hands is  degrees.
Notice that 60 = 60 degs corresponds to the position of the hour hand at 2:00 pm.
In 10 minutes, the minute hand will be in position of 6(t+10) degrees, while the hour hand will be in position of  degrees;
thus the angle between the hands will be  .
We should determine the time moment "t" by equating these two angles:
= . (1)
To solve the equation (1), multiply both sides by 12. You will get
12*6*(t+10) - 60*12 - 6*(t+10) = 60*12 + 6t - 12*6t.
Simplify:
12*6*t + 12*6*10 - 60*12 - 6t - 60 = 60*12 + 6t - 12*6t,
12*6*t - 6t - 6t + 12*6*t = 60*12 - 12*6*10 + 60*12 + 60,
132t = 780 ====> t =  = 5.909 minutes = 5 minutes 54.(54) seconds = 5 minute and 54.546 seconds (approximately).
Answer. The time under the question is 2 hours 5 minutes and 54.546 seconds (approximately; correct up-to 3 decimals after the decimal dot).
Solved.
|
|
|
