SOLUTION: Two recording devices are set 2600 feet apart, with the device at point A to the west of the device at point B. At a point on a line between the devices, 300 feet from point B, a s

Question 1089549: Two recording devices are set 2600 feet apart, with the device at point A to the west of the device at point B. At a point on a line between the devices, 300 feet from point B, a small amount of explosive is detonated. The recording devices record the time the sound reaches each one. How far directly north of site B should a second explosion be done so that the measured time difference recorded by the devices is the same as that for the first detonation?
Answer by Theo(13342) (Show Source): You can put this solution on YOUR website!
not sure if this is correct, but this is what i got.

it appears to be reasonable.

the distance between point A and B is 2600 feet.

the original sound is at a point 300 feet from point B.

this means it is 2300 feet from point A.

the difference in feet from the point of the sound to point A and the from the point of the sound to point B is 2000 feet.

since the sound always travels at the same speed, then if the difference in feet is the same, then the difference in the measured time should be the same.

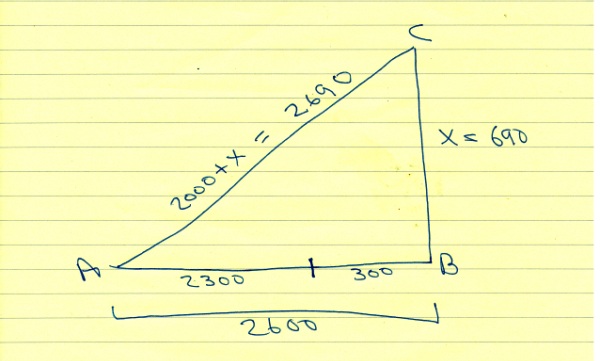
so you draw a triangle ABC

AB is equal to 2600

BC is equal to x

AC is equal to x + 2000.

you use the pythagorean formula to find the value of x and x + 2000.

x is equal to 690 and x + 2000 is equal to 2690.

the formula is 2600^2 + x^2 = (x + 2000)^2

the formula becomes 2600^2 + x^2 = x^2 + 4000x + 2000^2

the x^2 cancels out.

you then solve for x to get x = (2600^2 - 2000^2) / 4000 which is equal to 690.

x + 2000 then becomes 2690.

the speed of sound is irrelevant to this problem since it is the same for all distances.

assume the speed of sound is S.

since the source of the original sound is 300 feet from point B and 2300 feet from point A, then the difference in the time the sound reaches point B and point A would be 2300/S - 300/S which is equal to (2300 - 300) / S which is equal to 2000 / S.

if the new sound is at point C, then the time it takes for the sound to get to point A is 2690 / S and the time it takes for the sound to get to point A is 690 / S

the difference in the time is 2690 / S - 690 / S which is equal to (2690 - 690) / S which is equal to 2000 / S.

the difference is the same.

my diagram is shown below:

$$$

RELATED QUESTIONS
Two recording devices are set 2400 feet apart, with the device at point A to the west of... (answered by lynnlo)

A tracking device that is installed in a mobile phone indicates that its user is located... (answered by ikleyn)

Could you solve this problem for me I worked it out somewhat just want to know final... (answered by solver91311)

Assume that it costs a company approximately C(x) = 441,000 + 160x + 0.001x^2 dollars to (answered by ikleyn)

A ship using sound-sensing devices above and below water recorded a surface explosion 39... (answered by Paul)

A ship using sound-sensing devices above and below water recorded a surface explosion 39... (answered by ankor@dixie-net.com)

A car moving at a constant speed passed a timing device at t=0. After 9 seconds, the car... (answered by Alan3354)

I have two devices packaged together and each individual device yields 70% I need to... (answered by stanbon)

A smoke detector system uses two devices, A and B. Suppose the probability that it will... (answered by ikleyn)