one such calculator can be found here:
http://arachnoid.com/finance/index.html
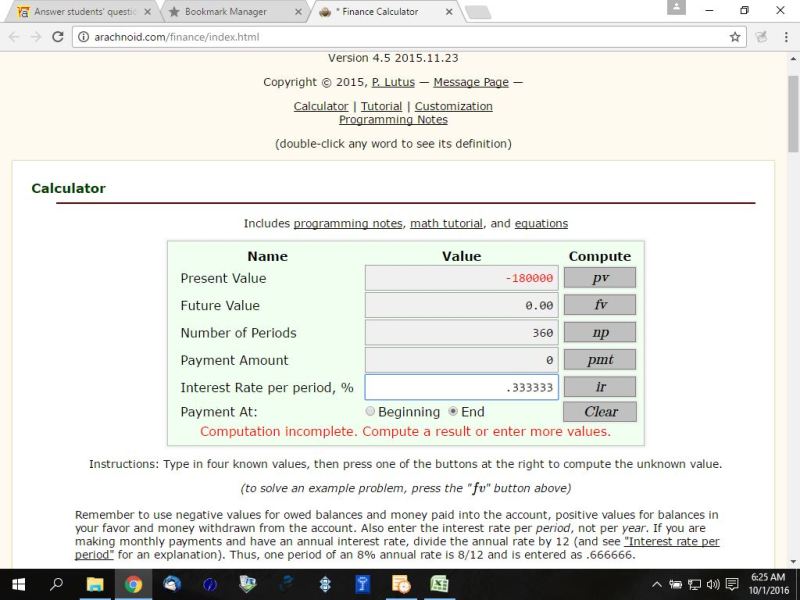
you would enter present value as -180,000
you would enter future value as 0.
you would enter interest rate at 4/12 percent = .333333
you would enter number of time periods as 30 * 12 = 360
you would enter payment as 0 or just leave it alone.
you would select end of period payments.
you would then select pmt and the calculator will tell you what the monthly payment is.
i truncated to 6 decimal digits which is usually enough accuracy to get a rough idea.
my inputs to this calculator look like this:
my output from the calculator look like this:

the calculator tells me that the monthly payment is 859.35.
i verified with another financial calculator that this is correct.
the month by month calculations are done as follows:
start with 180,000 as the mortgage amount.
that's the remaining balance at the beginning of the first month.
at the end of the first month the following happens:
interest = 4/1200 * 180,000 = 600.
payment = 859.35
principal reduction = 859.35 - 600 = 259.35
remaining balance = 179740.65.
at the end of the second month the following happens:
interest = 4/1200 * 179740.65 = 599.1355
payment = 859.35
principal reduction = 859.35 - 599.1355 = 260.2145
remaining balance = 179480.4355.
you do this for 4 months and you get:
month remaining balance interest payment principal 0 $180,000.00 $0.00 $0.00 $0.00 1 $179,740.65 $600.00 $859.35 $259.35 2 $179,480.44 $599.14 $859.35 $260.21 3 $179,219.36 $598.27 $859.35 $261.08 4 $178,957.41 $597.40 $859.35 $261.95
what you notice is that, as each month goes by, the interest part of the payment is less and the principal part of the payment is more.
this is because, as the remaining balance gets smaller, the interest on that remaining balance is smaller.
since the payment is a fixed amount each month, the principal part of the loan gets bigger.