324 is multiplied by a positive integer and the answer is both a perfect square and a perfect cube. What is the number used in the mulitiplication?
A number which is both a perfect square and a perfect cube is a
perfect sixth power:
 Any perfect 6th power is a product of perfect 6th powers. So to make a
perfect sixth power out of 324 by multiplying it by something,
we have to multiply it by 2 enough times to make it contain a factor
Any perfect 6th power is a product of perfect 6th powers. So to make a
perfect sixth power out of 324 by multiplying it by something,
we have to multiply it by 2 enough times to make it contain a factor
 , and we have to also multiply it by 3 enough times to make it
contain
, and we have to also multiply it by 3 enough times to make it
contain  So we have to multiply it by 2 four times, which amounts to multiplying
it by
So we have to multiply it by 2 four times, which amounts to multiplying
it by 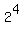 , and we also have to multiply it by 3 two times, which
amounts to multiplying it by
, and we also have to multiply it by 3 two times, which
amounts to multiplying it by  .
So we multiply 324 by
.
So we multiply 324 by  When we multiply 324 by 144 we get 46656 which is both
When we multiply 324 by 144 we get 46656 which is both  as well as
as well as  .
So the smallest possible answer is 144.
There are other answers too, but 144 is the smallest.
The next larger integer we could have used is to multiply 324 by 2 enough
times to make it a perfect twelfth power, which would be to multuiply it by
.
So the smallest possible answer is 144.
There are other answers too, but 144 is the smallest.
The next larger integer we could have used is to multiply 324 by 2 enough
times to make it a perfect twelfth power, which would be to multuiply it by
 When we multiply 324 by 9216 we get 2985984 which is both
When we multiply 324 by 9216 we get 2985984 which is both  as well as
as well as  .
There are actually an infinite number of correct answers, but I think
your teacher meant just the smallest answer, which is 144.
Edwin
.
There are actually an infinite number of correct answers, but I think
your teacher meant just the smallest answer, which is 144.
Edwin