Question 927192: what are rubas
Found 2 solutions by Fombitz, MathLover1:
Answer by Fombitz(32388)   (Show Source): (Show Source):
Answer by MathLover1(20849)   (Show Source): (Show Source):
You can put this solution on YOUR website! This is about   , in which a quantity grows larger or smaller at an , in which a quantity grows larger or smaller at an 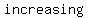  rather than at a rather than at a 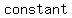  in linear relationships. in linear relationships.
Exponential growth is everywhere in the world. It isn't just counting how many Rubas a peasant gets from the king in a math book. One example of exponential growth in real life is allowance. Say your daily allowance is  cents. You make a deal with your parents to cents. You make a deal with your parents to  your allowance daily for your allowance daily for  days. It wouldn't seem like you were making much money at the start, but at the end of the days. It wouldn't seem like you were making much money at the start, but at the end of the  days, you would have made $ days, you would have made $ ! !
When I think about  life use for life use for  Relationships, I think about Relationships, I think about  . Taxes involve Exponential Relationships too. They have a specific pattern to them and if you follow it correctly you'll know how much your next bill will be. :) . Taxes involve Exponential Relationships too. They have a specific pattern to them and if you follow it correctly you'll know how much your next bill will be. :)
here is the story about rubas:
One day in the ancient kingdom of Montarek, a peasant saved the life of the king’s daughter. The king was so grateful he told the peasant she could have any reward she desired.
The peasant—who was also the kingdom’s chess champion—made an unusual request:
“I would like you to place  ruba on the first square of my chessboard, ruba on the first square of my chessboard,  rubas on the second square, rubas on the second square,  on the third square, on the third square,  on the fourth square, and so on, until you have covered all on the fourth square, and so on, until you have covered all  } squares. Each square should have } squares. Each square should have  as many rubas as the as many rubas as the  square.” square.”
The king replied, “Rubas are the least valuable coin in the kingdom. Surely you can think of a better reward.” But the peasant insisted, so the king agreed to her request.
Did the peasant make a wise choice?
think about this request:
 ruba on the first square of my chessboard, ruba on the first square of my chessboard,
 rubas on the second square, rubas on the second square,
 on the third square, on the third square,





 .......... .......... square square

:
:
and so on, up to  square square
an equation for the relationship between the number of the square n and the number of rubas,  is: is:
 or or 
Exponential vs Linear growth :-) life lesson: always try to choose better deal
|
|
|