Question 276236: use the exponential growth function, P(t)=Poe^kt, to find the value of k, then write the write the function for this population as a function of time, t.
1984= 746,388,000 1974=574,220,000 t=0 1974 t=10 1984
Answer by jsmallt9(3758)   (Show Source):
You can put this solution on YOUR website! 
In this equation 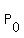 represents the population at time t = 0. In your case  . So the equation so far is:
Now we'll figure out k. We're also told that in 1984 the population was 746,388,000. In mathmatical terms: P(10) = 746,388,000. So we'll replace t with 10 and P(t) with 746,388,000:
or
Now we solve for k. With the variable in the exponent we will use logarithms to solve it. But before that, let's get rid of the number in front. IOW, divide both sides by 574220000:
Now we can use logarithms. The base of the logarithm we use is not significantly important. But it makes it easier if we use the same base as the base on which there is an exponent. So we want to use base e (i.e. ln) logarithms:
Next we use the property of logarithms,  , to move the exponent out in front. (This property is the whole reason we use logarithms. It is the best way to get the variable out of an exponent!). Using this property we can move the 10k out in front:
Since ln(e) = 1 by definition this simplifies to:
Dividing both sides by 10 we get:
We can reduce the fraction in the logarithm by a factor of 1000:
This is an exact expression for k. SO your final equation, with the exact value of k, is:
If you want a decimal approximation for k, then your need a calculator which "knows" ln logarithms.
 .
With this decimal approximation for k the equation looks like:
Of course you may prefer to round off the decimal approximation for k.
|
|
|
