Question 1204989: A population numbers 20,000 organisms initially and grows by 1.1% each year.
Suppose P represents population, and t the number of years of growth. An exponential model for the population can be written in the form P = a * b^t where a = ? and b = ?.
Found 2 solutions by Theo, math_tutor2020:
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! exponential equation is P = a * b ^ t
a would be equal to 20,000
b would be equal to 1 + .011 = 1.011
the equation would become P = 20,000 * 1.011 ^ t.
the equation can be graphed as shown below.
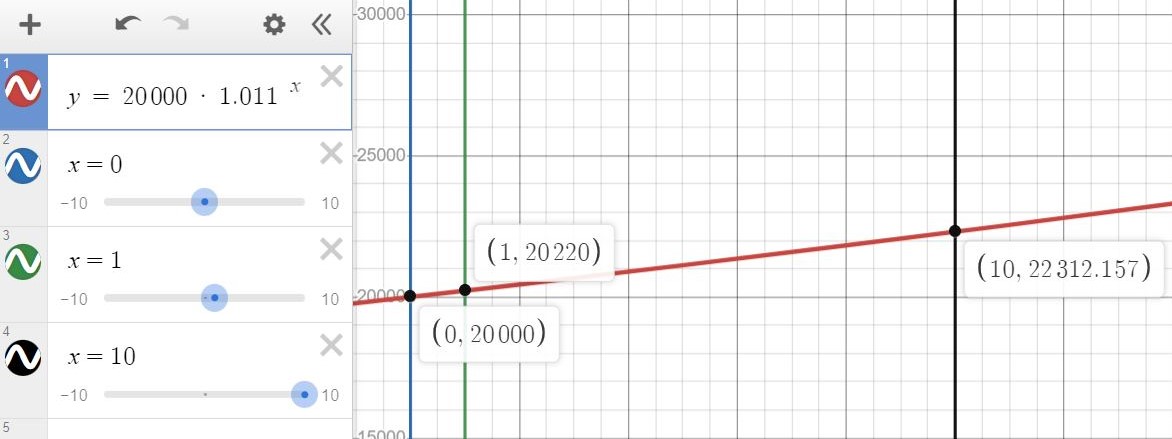
in the graph, x takes the place of t.
at x = 0, the value is 20,000 * 1.011 ^ 0 = 20,000
at x = 1, the value is 20,000 * 1.011 ^ 1 = 20220
at x = 10, the value is 20,000 * 1.011 ^ 10 = 22312.157 rounded to 3 decimal places, as in the graph.
to create b, you take 1.1% and divide it by 100 to get .011.
that's the decimal equivalent of 1.1%.
you then add 1 to it to get 1.011.
that becomes the growth factor.
20,000 * 1.011 is the same as 20,000 + 20,000 * .011.
factor out the 20,000 and you get 20,000 * (1 + .011) which becomes 20,000 * 1.011.
for 1 year out, the value becomes 20,000 * 1.011.
for 2 years out, the value becomes 20,000 * 1.011 * 1.011 which is equal to 20,000 * 1.011^2
10 years out is 20,000 * 1.011^10
Answer by math_tutor2020(3817)   (Show Source): (Show Source):
You can put this solution on YOUR website!
a = 20000 is the starting population
b = 1.011 to represent the 1.1% growth
b = 1+r, where r = 0.011 in this case
If b > 1 then we have exponential growth.
If 0 < b < 1, then there's exponential decay.
|
|
|