SOLUTION: The points A(-1,2),B(x,y) and C=(4,5) are such that BA=BC.Find a linear relation between x and y.

Algebra.Com
Question 550844: The points A(-1,2),B(x,y) and C=(4,5) are such that BA=BC.Find a linear relation between x and y.
Found 2 solutions by Theo, ikleyn:
Answer by Theo(13342)   (Show Source): You can put this solution on YOUR website!
point B will be any point on the perpendicular bisector of AC.
as such it will be equidistant between A and C which will always make AB = BC.
the linear relationship is the equation of the line that passes through the midpoint of AC and is perpendicular to it.
the equation of the line AC is:
y = (3/5)x + (13/5)
the equation of the line perpendicular to AC and passing through its midpoint is:
y = -(5/3)x + 6
the graph of the equations for those line is shown below:

point B is any point on the line perpendicular to AC, so the linear relationship between the x value of that point and the y value of that point is the equation of the line perpendicular to AC which is the equation:
y = -(5/3)x + 6.
a picture of the relationship is shown below:
$$$$$
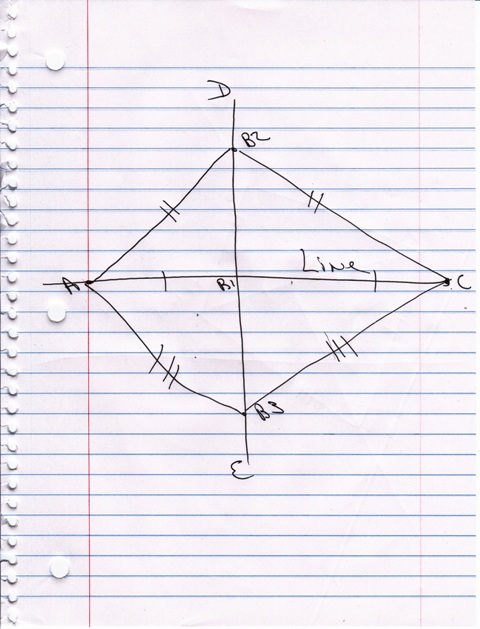
line DE is perpendiculat to line AC.
any point on line DE is equidistant from A and C.
Answer by ikleyn(52847)   (Show Source): You can put this solution on YOUR website!
.
The points A(-1,2), B(x,y) and C(4,5) are such that BA=BC. Find a linear relation between x and y.
~~~~~~~~~~~~~~~~~~~~~~~~~


        This problem has a nice Algebra solution. 


The square of the length of AB is 

    |AB|^2 = (x-(-1))^2 + (y-2)^2 = (x+1)^2 + (y-2)^2 = x^2 + 2x + 1 + y^2 - 4y + 4 = x^2 + 2x + y^2 - 4y + 5.



The square of the length of BC is 

    |BC|^2 = (x-4)^2 + (y-5)^2 = x^2 - 8x + 16 + y^2 - 10y + 25 = x^2 - 8x + y^2 - 10y + 41.



The condition  |BA| = |BC|  is the same as  |AB|^2 = |BC|^2.  It gives this equation 

    x^2 + 2x + y^2 - 4y + 5 = x^2 - 8x + y^2 - 10y + 41.



Combine like terms.  The final equation is

    10x + 6y = 36,

or

    5x + 3y = 18,

or

    y = .    <<<---===  ANSWER

Solved.



RELATED QUESTIONS

please help with homework 1) is the relation xy=5 a function within the domain(-5,-1)... (answered by stanbon)
I'm stuck with this problem, please help me? Take points A(7/2,0), B(0,7) and... (answered by venugopalramana)
Given the relation {(x,y): [x] + [y] = 1} where x and y are integers. A. Find the... (answered by Fombitz)
an ellipse x^2/(4c^2) + y^2/(c^2) = 1 and a circle x^2 + y ^2 = 9a^2 cuts at 4 points.... (answered by josgarithmetic)
Variables x and y are such that when lg(2y+1) is plotted against x^2, a straight line... (answered by proyaop)
Segment AB and segment BC are tangent to circle D. Find x if Segment AB = -x + 6 and (answered by ikleyn)
the points A(3,2) and B(2,-3) are equidistant from a point P(x,y). find the relation... (answered by josgarithmetic)
. Independent random variables X and Y are such that E X( ) 4  , E Y( ) 5  ,... (answered by CPhill)
I NEED HELP. PLEASE HELP ME ASAP. THANKS BEFORE :) 1) The straight line with equation... (answered by richard1234)