SOLUTION: find y if the distance between points p and R is 25 and point R is located in the first quadrant. P=(3,-8) R=(10,y)

Question 1139586: find y if the distance between points p and R is 25 and point R is located in the first quadrant.
P=(3,-8)
R=(10,y)
Found 4 solutions by ikleyn, MathLover1, Theo, greenestamps:
Answer by ikleyn(52777)   (Show Source): You can put this solution on YOUR website!
.

+ = + = 625 49 + = 625 = 625 - 49 = 576 y + 8 = +/- = +/- 24 y = -8 +/- 24. = -8 + 24 = 16; = -8 - 24 = -32. Only positive = 16 provides R is located in QI. ANSWER. y = 16.

Solved.

Answer by MathLover1(20849)   (Show Source): You can put this solution on YOUR website!

use distance formula:

given:
=(,)=(,)
=(,) =(,)
the distance between points and is

.......square both sides
......solve for

=> answer: =(,) which is located in the first quadrant

Answer by Theo(13342)   (Show Source): You can put this solution on YOUR website!
point p is at (3,-8)
point r is at (10,y)

the distance between them is 25.

point r is in the first quadrant.

this means that y has to be positive.

the distance between point p and point r is equal to sqrt((y+8)^2 + (10-3)^2).

simplify this to get distance between points p and r is equal to sqrt((y+8)^2 + 49)

since the distance between points p and r is 25, then the formula becomes:

25 = sqrt((y+8)^2 + 49)

square both sides of the equation to get 625 = (y+8)^2 + 49

simplify to get 625 = y^2 + 16y + 64 + 49

combine like terms to get 625 = y^2 + 16y + 113

subtract 625 from both sides of the equation to get 0 = y^2 + 16y - 512.

factor this quadratic equation to get (y + 32) * (y - 16) = 0

solve for y to get y = -32 or 16.

y is positive, so y has to be 16.

your solution is that y = 16.

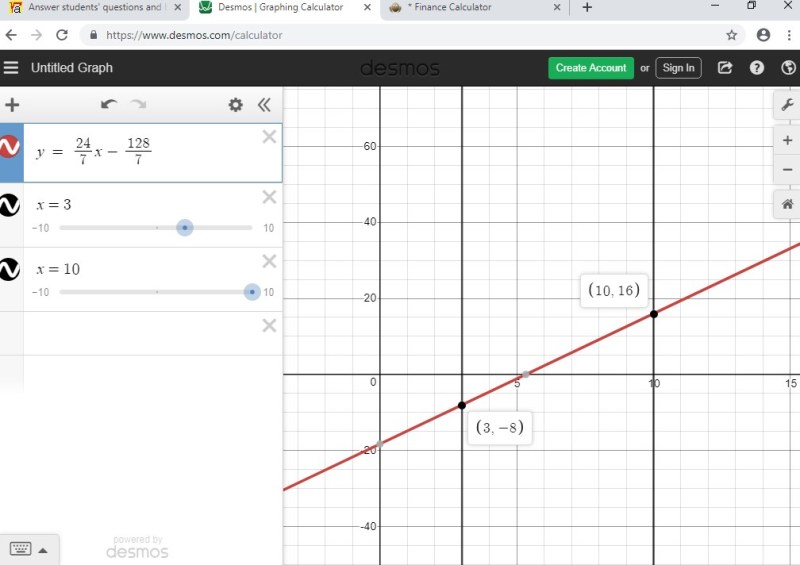
this means that point p = (3,-8) and point r = (10,16)

the distance between points p and r is equal to sqrt((16+8)^2 + (10-3)^2).

that becomes equal to sqrt((24)^2 + 7^2) which becomes equal to sqrt(625) which becomes equal to 25.

that confirms that, when y = 16, the distance between p and r is 25.

the equation of the line between points p and r is y = 24/7 * x -128/7.

the graph of that equation is shown below.

it shows that the points (3,-8) and (10,16) are both on the line, as they sh ould be.

Answer by greenestamps(13198)   (Show Source): You can put this solution on YOUR website!

The distance between the two points is 25; the difference between the x-coordinates is 7.

7-24-25 is a Pythagorean triple, so the difference between the y-coordinates must be 24.

If R is to be in the first quadrant, y must be -8+24 = 16.

ANSWER: y = 16
RELATED QUESTIONS
Point P is located at (3, 3) and Point Q is located at (1, 1). If Points P, Q and R are... (answered by josgarithmetic,MathTherapy)
Point P is located at (−2, 7) and point R is located at (1, 0). Find the y value... (answered by josgarithmetic)
If y = x² - 5x + 3 is expressed in the form y = p(x + q)² + r, where p, q and r are... (answered by josgarithmetic)
If y = 2x² - 5x + 3 is expressed in the form y = p(x + q)² + r, where p, q and r are... (answered by josgarithmetic)
If y = 2x² - 5x + 3 is expressed in the form y = p(x + q)² + r, where p, q and r are... (answered by josgarithmetic,solver91311)
1. If p, q, r are three points of a line and the coordinates of p and r are √3 and... (answered by ikleyn)
Points P, Q, and R lie in a plane. If the distance between P and Q is 5 and the distance... (answered by Fombitz,CharlesG2)
I have a triangle PQR. Point G is located between P&Q and point J is located between P&R. (answered by scott8148)