Question 751500: Find the equation of the circle that is inscribed in the triangle whose sides lie on the lines 3x+y=5,x-3y=1,and x+3y=-7.
Found 2 solutions by Edwin McCravy, AnlytcPhil:
Answer by Edwin McCravy(20055)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Given three lines, there are 4 circles which are tangent to all
three lines. There are three excircles and one inscribed circle
inside the triangle. Here they are:
 You only want the little red circle in the triangle, not the
3 excircles. However, we can't tell which of the four is the
inscribed circle. So we have to find them all.
Let the center of the circle be (h,k), and the radius r. Then the
equation of the circle is (x-h)² + (y-k)² = r²
We use the formula for perpendicular distance d
from the point whose coordinates are (x1,y1)
to the line whose equation is
Ax + By + C = 0
That is given by this formula:
d =
You only want the little red circle in the triangle, not the
3 excircles. However, we can't tell which of the four is the
inscribed circle. So we have to find them all.
Let the center of the circle be (h,k), and the radius r. Then the
equation of the circle is (x-h)² + (y-k)² = r²
We use the formula for perpendicular distance d
from the point whose coordinates are (x1,y1)
to the line whose equation is
Ax + By + C = 0
That is given by this formula:
d =  The perpendicular distances from the center to the three lines
are all equal, since they are all three radii.
So we find all three distances from the center (h,k) to the
three lines and we have:
We get 0 on the right side of the equations of the
three lines
3x+y=5, x-3y=1, and x+3y=-7
3x+y-5=0, x-3y-1=0, x+3y+7=0
Substituting in the formula above
r =
The perpendicular distances from the center to the three lines
are all equal, since they are all three radii.
So we find all three distances from the center (h,k) to the
three lines and we have:
We get 0 on the right side of the equations of the
three lines
3x+y=5, x-3y=1, and x+3y=-7
3x+y-5=0, x-3y-1=0, x+3y+7=0
Substituting in the formula above
r =  = =  = =  r =
r = 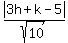 = =  = =  So we have this system of equations:
So we have this system of equations:
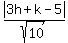 = = 
 = =  We multiply them both by √10
|3h + k - 5| = |h - 3k - 1|
|h - 3k - 1| = |h + 3k + 7|
There are four solutions to this system. Here are the four systems
We multiply them both by √10
|3h + k - 5| = |h - 3k - 1|
|h - 3k - 1| = |h + 3k + 7|
There are four solutions to this system. Here are the four systems
 , ,  , ,  , ,  Those simplify to
Those simplify to
 , ,  , ,  , , Their solutions are
(
Their solutions are
(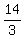 ,-4/3), (-3, ,-4/3), (-3, ), ( ), ( , ,  ), (-3,-9)
To find the radii, we substitute each of those in:
r = ), (-3,-9)
To find the radii, we substitute each of those in:
r = 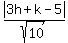 I'll just find the radius of the small red circle since that's
the only one you were asked to find.
It is the circle with the center (
I'll just find the radius of the small red circle since that's
the only one you were asked to find.
It is the circle with the center ( , ,  ).
r = ).
r =  r =
r =  Multiply top and bottom by 6
r =
Multiply top and bottom by 6
r =  r =
r =  r =
r =  r² =
r² =  r² =
r² =  Substituting in
(x-h)² + (y-k)² = r²
(x-
Substituting in
(x-h)² + (y-k)² = r²
(x- )² + (y-( )² + (y-( ))² = ))² =  (x-
(x- )² + (y+ )² + (y+ )² = )² =  Or you can multiply that out and simplify it in general form
and get:
360x² + 360y² - 600x + 960y + 361 = 0
It doesn't come out very nice but it's correct.
Edwin
Or you can multiply that out and simplify it in general form
and get:
360x² + 360y² - 600x + 960y + 361 = 0
It doesn't come out very nice but it's correct.
Edwin
Answer by AnlytcPhil(1806)   (Show Source): (Show Source):
You can put this solution on YOUR website! Question 751500
Given three lines, there are 4 circles which are tangent to all
three lines. There are three excircles and one inscribed circle
inside the triangle. Here they are:
 You only want the little red circle in the triangle, not the
3 excircles. However, we can't tell which of the four is the
inscribed circle. So we have to find them all.
Let the center of the circle be (h,k), and the radius r. Then the
equation of the circle is (x-h)² + (y-k)² = r²
We use the formula for perpendicular distance d
from the point whose coordinates are (x1,y1)
to the line whose equation is
Ax + By + C = 0
That is given by this formula:
d =
You only want the little red circle in the triangle, not the
3 excircles. However, we can't tell which of the four is the
inscribed circle. So we have to find them all.
Let the center of the circle be (h,k), and the radius r. Then the
equation of the circle is (x-h)² + (y-k)² = r²
We use the formula for perpendicular distance d
from the point whose coordinates are (x1,y1)
to the line whose equation is
Ax + By + C = 0
That is given by this formula:
d =  The perpendicular distances from the center to the three lines
are all equal, since they are all three radii.
So we find all three distances from the center (h,k) to the
three lines and we have:
We get 0 on the right side of the equations of the
three lines
3x+y=5, x-3y=1, and x+3y=-7
3x+y-5=0, x-3y-1=0, x+3y+7=0
Substituting in the formula above
r =
The perpendicular distances from the center to the three lines
are all equal, since they are all three radii.
So we find all three distances from the center (h,k) to the
three lines and we have:
We get 0 on the right side of the equations of the
three lines
3x+y=5, x-3y=1, and x+3y=-7
3x+y-5=0, x-3y-1=0, x+3y+7=0
Substituting in the formula above
r =  = =  = =  r =
r = 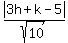 = =  = =  So we have this system of equations:
So we have this system of equations:
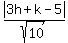 = = 
 = =  We multiply them both by √10
|3h + k - 5| = |h - 3k - 1|
|h - 3k - 1| = |h + 3k + 7|
There are four solutions to this system. Here are the four systems
We multiply them both by √10
|3h + k - 5| = |h - 3k - 1|
|h - 3k - 1| = |h + 3k + 7|
There are four solutions to this system. Here are the four systems
 , ,  , ,  , ,  Those simplify to
Those simplify to
 , ,  , ,  , , Their solutions are
(
Their solutions are
(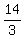 ,-4/3), (-3, ,-4/3), (-3, ), ( ), ( , ,  ), (-3,-9)
To find the radii, we substitute each of those in:
r = ), (-3,-9)
To find the radii, we substitute each of those in:
r = 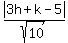 I'll just find the radius of the small red circle since that's
the only one you were asked to find.
It is the circle with the center (
I'll just find the radius of the small red circle since that's
the only one you were asked to find.
It is the circle with the center ( , ,  ).
r = ).
r =  r =
r =  Multiply top and bottom by 6
r =
Multiply top and bottom by 6
r =  r =
r =  r =
r =  r² =
r² =  r² =
r² =  Substituting in
(x-h)² + (y-k)² = r²
(x-
Substituting in
(x-h)² + (y-k)² = r²
(x- )² + (y-( )² + (y-( ))² = ))² =  (x-
(x- )² + (y+ )² + (y+ )² = )² =  Or you can multiply that out and simplify it in general form
and get:
360x² + 360y² - 600x + 960y + 361 = 0
It doesn't come out very nice but it's correct.
Edwin
Or you can multiply that out and simplify it in general form
and get:
360x² + 360y² - 600x + 960y + 361 = 0
It doesn't come out very nice but it's correct.
Edwin
|
|
|