Question 563793: The larger circle circumscribes an equilateral triangle, which circumscribes a small circle. The area of the larger circle is 12pi. What is the triangle's perimeter. I not sure how to do this problem and how to work it out.
Found 2 solutions by Theo, ikleyn:
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! i can solve this using trigonometry
i don't know how to solve it otherwise,
using trigonometry i would do the following:
the area of the larger circle is equal to 12*pi
since the area of a circle is equal to pi*r^2, this means that:
the radius of the circle = sqrt(12)
the radii of the big circle in the diagram are:
DB, DC, DA
the radii of the small circle in the diagram are:
DE, DF, DG
these radii are also the apothems of the triangle.
the apothems of the triangle intersect the sides of the triangle at a right angle.
this forms 8 right triangles.
they are:
DBF, DFC, DCG, DGA, DAE, DEB
the hypotenuse of each of these 8 triangles are the radii of the large circle.
this makes their length equal to sqrt(12)
the angle of each of these triangles with a vertex at the center of the circle is equal to 60 degrees.
using trigonometry, you can calculate the distance of the legs of these triangles that form the perimeter of the larger triangle which is an equilateral triangle and is labeled ABC.
using right triangle DBF:
the hypotenuse is DB with a length of sqrt(12)
the angle is BDF which is 60 degrees.
the sine of angle BDF is equal to opposite / hypotenuse which is equal to BF / BD
since BD is equal to sqrt(12), then we get:
sine (BDF) is equal to BF / sqrt(12)
multiply both sides of this equation by sqrt(12) to get:
BF = sqrt(12) * sine(BDF)
since angle BDF is 60 degrees, we get:
BF = sqrt(12) * sine (60) which becomes:
BF = 3
2 * 3 is equal to the length of one of the sides of the equilateral triangle.
3 * 2 * 3 is equal to the perimeter of the equilateral triangle.
that perimeter is equal to 18.
the diagram is shown below:

Answer by ikleyn(52813)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The larger circle circumscribes an equilateral triangle, which circumscribes a small circle.
The area of the larger circle is 12pi. What is the triangle's perimeter.
I not sure how to do this problem and how to work it ou
~~~~~~~~~~~~~~~~~~~~~~~~~~
In this problem, the smaller circle is irrelevant, so we can omit any mention about it.
Therefore, I will reformulate the problem by removing everything that does not matter:
The circle circumscribes an equilateral triangle. The area of the circle is 12pi.
What is the triangle's perimeter ?
Below is the solution for this modified formulation.
For any triangle with the side lengths 'a', 'b' and 'c', the radius of the circumscribed circle is
R =  , (1)
where A is the area of the triangle. In our case, all three sides are congruent a = b = c,
so the radius of the circumscribed circle is
R = , (1)
where A is the area of the triangle. In our case, all three sides are congruent a = b = c,
so the radius of the circumscribed circle is
R =  . (2)
The area of the circumscribed circle is A = . (2)
The area of the circumscribed circle is A = 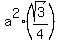 square units.
Substituting it into the formula (1), we get
R = square units.
Substituting it into the formula (1), we get
R =  = =  . (3)
We are given that the area of the circle is . (3)
We are given that the area of the circle is  , so we can write this equation , so we can write this equation
 = =  .
Cancel .
Cancel 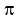 in both sides to get in both sides to get
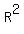 = 12.
Substitute here R from (3). You will get = 12.
Substitute here R from (3). You will get
 = 12.
Simplify and find 'a' = 12.
Simplify and find 'a'
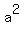 = 3*12 = 36, a = = 3*12 = 36, a =  = 6 units.
Hence, the perimeter of the triangle is 3*6 = 18 units.
ANSWER. The perimeter of the triangle is 18 units. = 6 units.
Hence, the perimeter of the triangle is 3*6 = 18 units.
ANSWER. The perimeter of the triangle is 18 units.
Thus we produced short, straightforward, compact and elegant Geometry solution.
|
|
|