SOLUTION: Find at least two values for θ that fit the equation sin θ = 0.5√3. How many such values are there?

Algebra ->  Circles -> SOLUTION: Find at least two values for θ that fit the equation sin θ = 0.5√3. How many such values are there?      Log On


   

Question 1163364: Find at least two values for θ that fit the
equation sin θ = 0.5√3. How many such values are there?
Found 2 solutions by ikleyn, Theo:
Answer by ikleyn(52800) About Me  (Show Source):
You can put this solution on YOUR website!
.

This equation  sin%28theta%29 = sqrt%283%29%2F2  has two solutions in the interval [0,2pi):


    theta = pi%2F3,   or  60 degrees,

and

    theta = %282pi%29%2F3,   or 120 degrees.


If there are not restrictions and the entire number line is considered as a domain for the equation, 
then it has INFINITELY many solutions, distinct from the two found solutions by the full angle multiple of 2pi.


Answer by Theo(13342) About Me  (Show Source):
You can put this solution on YOUR website!
sin(theta) = 0.5 * sqrt(3) which is the same as sqrt(3) / 2
that should be sin(60) if i remember correctly.
i just verified that it is.
so we're talking about 60 degrees in the first quadrant.
since sine is positive in the first and second quadrant, then the other angle between 0 and 360 degrees would be 180 minus 60 = 120 degrees.
the other quadrants between 0 and 360 degrees have angles with the same value, except they're negative.
angle in the third quadrant would be 180 + 60 = 240.
angle in the fourth quadrant would be 360 - 60 = 300.
so you have two angles between 0 and 360 that have a sine of sqrt(3)/2.
they are 60 and 120.
that's between 0 and 360.
those angles repeat every 360 degrees, so.
60 plus or minus k * 360 degrees and 120 plus or minus k * 360 degrees where k is an integer that is greater than or equal to 0.
here's a graph of the angles that have sqrt(3)/2 for their sine between -360 and 720 degrees.



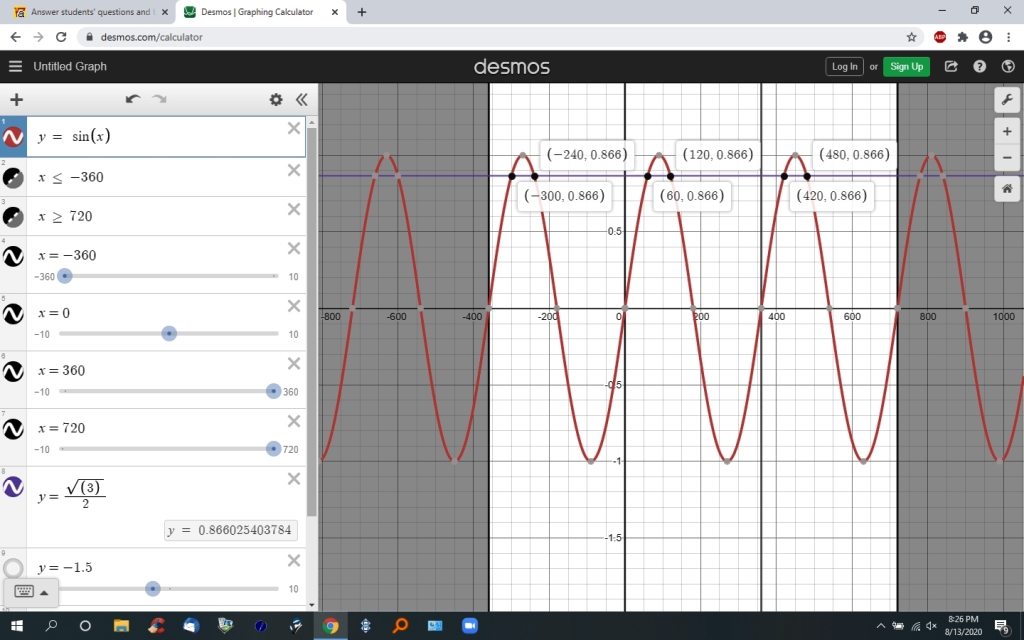
you will see that sine(x) = sqrt(3)/2 for the following angles.
60 + 0 * 360 = 60
60 + 1 * 360 = 420
120 + 0 * 360 = 120
120 + 1 * 360 = 480
60 - 1 * 360 = -300
120 - 1 * 360 = -240
when we go from left to right on the graph, we should see sin(x) = .866 at the following degrees.
-300, -240, 60, 120, 420, 480
the graph shows the intersections in (x,y) format.
x is the angle,
y is the sine.
.866 is equal to sqrt(3)/2 rounded to 3 decimal place.
there are two angles in the 0 to 360 degree range.
there are an infinite number angles when there is no restriction on the number of degrees to include in the set.
this was mentioned above, and is repeated her for your convenience.
those angles repeat every 360 degrees, so......:
60 plus or minus k * 360 degrees and 120 plus or minus k * 360 degrees where k is an integer that is greater than or equal to 0.