Question 1143644: A point O is inside a square lot. If the distances from point O to the three successive corners of the square lot are 5m, 3m, 4m respectively. Determine the area of the square lot.
--can you plss draw the fig.
Answer by ikleyn(52855)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Take a page of paper and a pen or a pencil and plot it on your own.
We are not an art studio to make plots for you.
Instead of plotting the figure, I will solve the problem, from the beginning to the end. OK ?
.
Let ABCD be the square with the side of the length "a" in a coordinate plane,
A = (0,0), B = (a,0), C = (a,a) and D = (0,a).
Let (x,y) be the point inside the square ABCD with the distance 3 from A, 4 from D and 5 from B.
Then we have these three equations ("distances")
x^2 + y^2 = 3^2, (1)
(a-x)^2 + y^2 = 5^2, (2)
x^2 + (y-a)^2 = 4^2. (3)
Making FOIL in equations (2) and (3), I can re-write (1), (2) and (3) in this form
x^2 + y^2 = 9, (4) (= same as (1) )
a^2 - 2ax + x^2 + y^2 = 25, (5)
x^2 + y^2 - 2ay + a^2 = 16. (6)
Replacing x^2 + y^2 by 9 in equations (5) and (6), I obtain new equations instead of them
a^2 - 2ax = 16 (7)
a^2 - 2ay = 7 (8)
From equations (7) and (8), x = 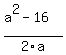 , y = , y = 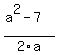 .
Substituting these expressions for x and y into equation (4), you get .
Substituting these expressions for x and y into equation (4), you get
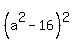 + + 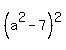 = = 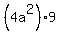 ,
or, simplifying ,
or, simplifying
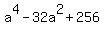 + + 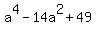 = {{36a^2}}}, = {{36a^2}}},
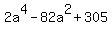 = 0.
From this bi-quadratic equation, you get for = 0.
From this bi-quadratic equation, you get for  , by applying the quadratic formula , by applying the quadratic formula
 = =  = =  .
The smaller value does not work for "a" (as it is easy to check), leaving the larger value .
The smaller value does not work for "a" (as it is easy to check), leaving the larger value
 = =  as the only meaningful.
Thus the area of the square is
as the only meaningful.
Thus the area of the square is  = =  = 36.863 square units (approximately). = 36.863 square units (approximately).
Solved.
=============
It is not for the first time such problem comes to the forum.
Some time ago I solved similar problem here under this link
https://www.algebra.com/algebra/homework/Parallelograms/Parallelograms.faq.question.1135915.html
https://www.algebra.com/algebra/homework/Parallelograms/Parallelograms.faq.question.1135915.html
/\/\/\/\/\/\/\/
Thanks for posting this interesting problem.
It was a pleasure for me to solve it again (even for the second time), because the solution is nice.
|
|
|