Question 1093746: The center of a circle is located at O(1, h). The line whose equation is y=kx+1 is tangent to circle O at the point P(3,6). Find the values of k and h.
I'm trying to learn how to do this for myself, so would you show work, please?
Found 2 solutions by greenestamps, Edwin McCravy:
Answer by greenestamps(13200)   (Show Source):
You can put this solution on YOUR website!
Drawing a rough sketch is a huge help in visualizing the problem, and in getting an idea of how to solve the problem. I will let you do most of the actual calculations; I will just describe the process I would use to solve the problem.
Start by plotting the point P(3,6). That is a very important point in the problem, since it is the point where the line y = kx+1 is tangent to the circle.
Next, we know that the given line y=kx+1 has y-intercept (0,1). That gives us two points on the line, so it is easy to find the equation of the line. Sketch the line passing through the points (0,1) and (6,3). The slope between (0,1) and (3,6) is 5/3, so the equation of the line is y = (5/3)x+1.
If the line is tangent to the circle, then the tangent is perpendicular to a radius of the circle. Since the radius and the tangent are perpendicular to each other, and the slope of the tangent is 5/3, the slope of the radius is -3/5. Sketch a line perpendicular to the tangent line at (3,6); the center of the circle will lie somewhere on that line.
Now you have two points that are on the radius of the circle, so you can find the equation of the line that contains the radius.
Finally, you want to know the y coordinate of the center of the circle, given that the x coordinate is 1. Simply plug x=1 into the equation of the line containing the radius to get that answer.
Answer by Edwin McCravy(20060)  (Show Source):
You can put this solution on YOUR website!
Comparing with the slope intercept form y=mx+b, the tangent line IP
whose equation is y=kx+1 has y-intercept (0,b) = I(0,1), and
slope m=k.
Since the line goes through I(0,1) and P(3,6), we use the
slope formula to determine m = k, its slope:
 <-- that's the answer for k
The radius OP is perpendicular to line IP, so its slope is
the reciprocal of  with the opposite sign, so the
slope of the radius OP is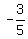 
To find the equation of OP, we use the point-slope form of
a line with  and the point of tangency, P(3,6).
 <--equation of radius OP
Since center O(1,h) is on that radius, we substitute the
point (1,h), to find h
 <---that's the answer for h
Edwin
|
|
|
