Question 1077722: there exist two circles that go through two points (1,3); (2,4) and are tangent to the y-axis. Letting the radii of the circles be a, b implies that ab=?
*do not graph
Answer by ikleyn(52794)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
there exist two circles that go through two points (1,3); (2,4) and are tangent to the y-axis.
Letting the radii of the circles be a, b implies that ab=?
*do not graph
~~~~~~~~~~~~~~~~~~~~~~
The solution would be much easier to understand having a plot.
But, since you directly and explicitly ask do not graph, I will not use it.
1. Draw (mentally) the segment connecting the given points (1,3) and (2,4).
This segment has the slope 1 = 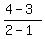 .
The centers of the two circles lie in the perpendicular bisector to this segment.
The perpendicular bisector goes through the middle point (1.5,3.5) and has the slope -1.
2. Let us find the radius of the "upper" circle.
Let "p" be the distance along the perpendicular bisector from the middle point (1.5,3.5) to the center of the "upper" circle.
Then the center of the "upper" circle is at the point ( .
The centers of the two circles lie in the perpendicular bisector to this segment.
The perpendicular bisector goes through the middle point (1.5,3.5) and has the slope -1.
2. Let us find the radius of the "upper" circle.
Let "p" be the distance along the perpendicular bisector from the middle point (1.5,3.5) to the center of the "upper" circle.
Then the center of the "upper" circle is at the point (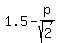 , ,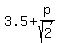 ), and the radius of the upper circle is ), and the radius of the upper circle is 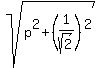 .
Since the upper circle touches y-axis, it gives the equation for "p" .
Since the upper circle touches y-axis, it gives the equation for "p"
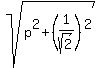 = = 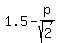 .
From this equation, p = (square both sides; simplify; then apply the quadratic formula) = .
From this equation, p = (square both sides; simplify; then apply the quadratic formula) =  .
Then the radius of the upper circle is .
Then the radius of the upper circle is  = =  = 1, which gives a = 1. (1)
3. Now, let us find the radius of the "lower" circle.
Let "q" be the distance along the perpendicular bisector from the middle point (1.5,3.5) to the center of the "lower" circle.
Then the center of the "lower" circle is at the point ( = 1, which gives a = 1. (1)
3. Now, let us find the radius of the "lower" circle.
Let "q" be the distance along the perpendicular bisector from the middle point (1.5,3.5) to the center of the "lower" circle.
Then the center of the "lower" circle is at the point (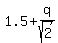 , ,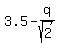 ), and the radius of the lower circle is ), and the radius of the lower circle is 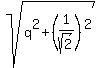 .
Since the lower circle touches y-axis, it gives the equation for "q" .
Since the lower circle touches y-axis, it gives the equation for "q"
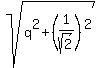 = = 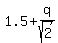 .
From this equation, q = (square both sides; simplify; then apply the quadratic formula) = .
From this equation, q = (square both sides; simplify; then apply the quadratic formula) = 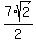 .
Then the radius of the upper circle is .
Then the radius of the upper circle is  = = 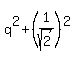 = = 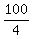 = 25, which gives b = = 25, which gives b =  = 5. (2)
3. From (1) and (2), a*b = 1*5 = 5. = 5. (2)
3. From (1) and (2), a*b = 1*5 = 5.
Answer. The product a*b under the question is 5.
Now, finally, I use all that I got and illustrate these results in the plot below.
It is my CHECK !

*** SOLVED ! ***
|
|
|