Question 1034430: Two parallel chords, one 10 and the other 16 and 13 units apart. Find the diameter.
Answer by ikleyn(52858)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Two parallel chords, one 10 and the other 16 and 13 units apart. Find the diameter.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Unclear.
Read your post.
How many chords?
------------------------------------------------
Comment from student: The first thing I said was two chords, there 2 on opposite sides of the circle.
The one closer to the top is 10 units and the bottom chord is 16. The chords are 13 units apart.
------------------------------------------------
My response:
First formulation was BAD. The second makes things clearer, although is not perfect.
But let us turn to the solution.
Please make a sketch. Draw the diameter parallel to the chords.
There are TWO possible configurations.
1) The chords are in one side of the diameter.
2) The chords are in different sides.
I will consider here only the configuration #1, leaving #2 to you.
Let "x" be the distance from the center to the first chord and "y" be the distance from the center to the first chord.
Then you have this system of 3 equations
x + y = 13, (1) (in configuration #2 it is x - y = 13)
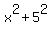 = =  , (2) , (2)
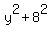 = =  . (3)
Here 5 in (2) is half of 10, while 8 in (3) is half of 16.
Distract equation (3) from (2) (both sides). You will get . (3)
Here 5 in (2) is half of 10, while 8 in (3) is half of 16.
Distract equation (3) from (2) (both sides). You will get
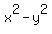 = = 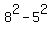 , or
(x+y)*(x-y) = 64 - 25, or
(x+y)*(x-y) = 39. (4)
In (4), replace x+y by 13 due to (1). You will get
x - y = , or
(x+y)*(x-y) = 64 - 25, or
(x+y)*(x-y) = 39. (4)
In (4), replace x+y by 13 due to (1). You will get
x - y = 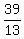 = 3.
Now you have two equations:
x + y = 13. ( it is former equation (1) )
x - y = 3.
Add them to get 2x = 16 and x = 8.
Then y = 5.
The problem is solved (in half, i.e. for configuration #1).
For #2 please do it yourself following the same scheme. = 3.
Now you have two equations:
x + y = 13. ( it is former equation (1) )
x - y = 3.
Add them to get 2x = 16 and x = 8.
Then y = 5.
The problem is solved (in half, i.e. for configuration #1).
For #2 please do it yourself following the same scheme.
|
|
|