SOLUTION: Before she took her last exam, the average of Tara’s exam scores was 89. She figures that if she scores 97 on the last exam, her average for all the exams will be 90. If she scor

Algebra ->  Average -> SOLUTION: Before she took her last exam, the average of Tara’s exam scores was 89. She figures that if she scores 97 on the last exam, her average for all the exams will be 90. If she scor      Log On


   

Question 320796: Before she took her last exam, the average of Tara’s exam scores was 89. She figures that if she scores 97 on the last exam, her average for all the exams will be 90. If she scores a 73, her average for all the exams will be 87. How many exams, including the last one, are given in the class?

Found 2 solutions by solver91311, Edwin McCravy:
Answer by solver91311(24713) About Me  (Show Source):
You can put this solution on YOUR website!


This is a problem where you have an embarrassment of riches as far as given information goes. Actually it is sufficient to know that the current average is 89 and a 97 on the last exam will result in an overall average of 90 to answer the question "How many exams...?"

Let represent the total number of exams, including the last one. That means that up until now, exams have been given. Hence, if the average for the exams already given is 89, then the sum of the scores of the exams already given must be .

The average of all the exams is then the sum of the first exams plus 97 all divided by and that is equal to 90.



Multiply by







Therefore 8 total exams.

Check.

Seven times 89 is 623. 623 plus 97 is 720. 720 divided by 8 is 90.

Further check.

Seven times 89 is 623. 623 plus 73 is 696. 696 divided by 8 is 87.

John

Answer by Edwin McCravy(20059) About Me  (Show Source):
You can put this solution on YOUR website!

[The other tutor ignored the extra information which caused the problem
to be inconsistent, thus he didn't notice that the extra information
caused the problem to be inconsistent.]

Before she took her last exam, the average of Tara’s exam scores was 89. She
figures that if she scores 97 on the last exam, her average for all the exams
will be 90. If she scores a 73, her average for all the exams will be
87. How many exams, including the last one, are given in the class? 

Something is wrong with this problem.  There is too much information given,
and the extra information causes an inconsistency, as we will see.
The average equation is:

Average%22=%22%28Sum_of_all_scores%29%2F%28Number_of_scores%29

Let S%22=%22Sum_of_all_scores_before_last-exam%29
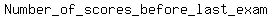Let N%22=%22Number_of_scores_before_last_exam

So, using the equation for the scores before the last exam,

89%22=%22S%2FN

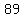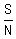And, using the formula for after the last exam, assuming she scores 97 on   
the (N+1)st exam. we add 97 to the sum S and 1 to the number of exams N

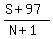90%22=%22%28S%2B97%29%2F%28N%2B1%29

Also, using the formula for after the last exam, assuming she scores 73 on   
the (N+1)st exam. we add 73 to the sum S and 1 to the number of exams N.

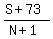87%22=%22%28S%2B73%29%2F%28N%2B1%29

So we have the system:

system%2889=S%2FN%2C+90=%28S%2B97%29%2F%28N%2B1%29%2C+87=%28S%2B73%29%2F%28N%2B1%29%29

This has more equations than there are unknowns!

Simplifying:

system%28S=89N%2C+%28S%2B97%29=90%28N%2B1%29%2C+%28S%2B73%29=87%28N%2B1%29%29

Simplifying further:

system%28S-89N=0%2C+S%2B97=90N%2B90%2CS%2B74=87N%2B87%29

system%28S-89N=0%2C+S-90N=-7%2CS-87N=13%29

If we ignore the third equation, and just use the first two:

system%28S-89N=0%2C+S-90N=-7%29

We get S= 623 and N=7, so there were 7 exams before the last
one, and 8 exams after the last one.

If we ignore the second equation, and just use the first and
third ones:

system%28S-89N=0%2C+S-87N=13%29

We get S= 578.5 and N=6.5, so there were 6.5 exams before the last
one, and 7.5 exams after the last one.  That is impossible because
we cannot have "half a test".

If we ignore the first equation, and just use the second and
third ones:

system%28S-90N=-7%2CS-87N=13%29

We get S= 593 and N=6%262%2F3, so there were 6%262%2F3 exams before the last
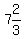one, and 7%262%2F3 exams after the last one.  That is impossible because
you cannot have "two-thirds of a test".

So the culprit is that second equation which comes from the sentence

If she scores a 73, her average for all the exams will be 87.

Therefore the problem would have been just fine if you had left off the
sentence "If she scores a 73, her average for all the exams will be 87."
That sentence ruins the problem, because the equation it represents
is inconsistent with the other two.

So the problem should read:

Before she took her last exam, the average of Tara’s exam scores was 89. She
figures that if she scores 97 on the last exam, her average for all the exams
will be 90. If she scores a 73, her average for all the exams will be
87. How many exams, including the last one, are given in the class?

Then the problem has a solution, 8.  But with that sentence I have lined
through, the problem is inconsistent.  You should let your teacher know this.

Edwin