Question 1062142: Three fair six-sided number cubes, each with faces labeled 0,2,4,6,8,10 are all rolled. What is the probability that the sum of the numbers rolled is greater than 20? Express your answer with a common fraction.
Found 4 solutions by Fombitz, Boreal, KMST, MathTherapy:
Answer by Fombitz(32388)   (Show Source): (Show Source):
You can put this solution on YOUR website! Here's a list of all possible outcomes, 3 face values and sum.
.
.
.
0 0 0 0
0 0 2 2
0 0 4 4
0 0 6 6
0 0 8 8
0 0 10 10
0 2 0 2
0 2 2 4
0 2 4 6
0 2 6 8
0 2 8 10
0 2 10 12
0 4 0 4
0 4 2 6
0 4 4 8
0 4 6 10
0 4 8 12
0 4 10 14
0 6 0 6
0 6 2 8
0 6 4 10
0 6 6 12
0 6 8 14
0 6 10 16
0 8 0 8
0 8 2 10
0 8 4 12
0 8 6 14
0 8 8 16
0 8 10 18
0 10 0 10
0 10 2 12
0 10 4 14
0 10 6 16
0 10 8 18
0 10 10 20
2 0 0 2
2 0 2 4
2 0 4 6
2 0 6 8
2 0 8 10
2 0 10 12
2 2 0 4
2 2 2 6
2 2 4 8
2 2 6 10
2 2 8 12
2 2 10 14
2 4 0 6
2 4 2 8
2 4 4 10
2 4 6 12
2 4 8 14
2 4 10 16
2 6 0 8
2 6 2 10
2 6 4 12
2 6 6 14
2 6 8 16
2 6 10 18
2 8 0 10
2 8 2 12
2 8 4 14
2 8 6 16
2 8 8 18
2 8 10 20
2 10 0 12
2 10 2 14
2 10 4 16
2 10 6 18
2 10 8 20
2 10 10 22
4 0 0 4
4 0 2 6
4 0 4 8
4 0 6 10
4 0 8 12
4 0 10 14
4 2 0 6
4 2 2 8
4 2 4 10
4 2 6 12
4 2 8 14
4 2 10 16
4 4 0 8
4 4 2 10
4 4 4 12
4 4 6 14
4 4 8 16
4 4 10 18
4 6 0 10
4 6 2 12
4 6 4 14
4 6 6 16
4 6 8 18
4 6 10 20
4 8 0 12
4 8 2 14
4 8 4 16
4 8 6 18
4 8 8 20
4 8 10 22
4 10 0 14
4 10 2 16
4 10 4 18
4 10 6 20
4 10 8 22
4 10 10 24
6 0 0 6
6 0 2 8
6 0 4 10
6 0 6 12
6 0 8 14
6 0 10 16
6 2 0 8
6 2 2 10
6 2 4 12
6 2 6 14
6 2 8 16
6 2 10 18
6 4 0 10
6 4 2 12
6 4 4 14
6 4 6 16
6 4 8 18
6 4 10 20
6 6 0 12
6 6 2 14
6 6 4 16
6 6 6 18
6 6 8 20
6 6 10 22
6 8 0 14
6 8 2 16
6 8 4 18
6 8 6 20
6 8 8 22
6 8 10 24
6 10 0 16
6 10 2 18
6 10 4 20
6 10 6 22
6 10 8 24
6 10 10 26
8 0 0 8
8 0 2 10
8 0 4 12
8 0 6 14
8 0 8 16
8 0 10 18
8 2 0 10
8 2 2 12
8 2 4 14
8 2 6 16
8 2 8 18
8 2 10 20
8 4 0 12
8 4 2 14
8 4 4 16
8 4 6 18
8 4 8 20
8 4 10 22
8 6 0 14
8 6 2 16
8 6 4 18
8 6 6 20
8 6 8 22
8 6 10 24
8 8 0 16
8 8 2 18
8 8 4 20
8 8 6 22
8 8 8 24
8 8 10 26
8 10 0 18
8 10 2 20
8 10 4 22
8 10 6 24
8 10 8 26
8 10 10 28
10 0 0 10
10 0 2 12
10 0 4 14
10 0 6 16
10 0 8 18
10 0 10 20
10 2 0 12
10 2 2 14
10 2 4 16
10 2 6 18
10 2 8 20
10 2 10 22
10 4 0 14
10 4 2 16
10 4 4 18
10 4 6 20
10 4 8 22
10 4 10 24
10 6 0 16
10 6 2 18
10 6 4 20
10 6 6 22
10 6 8 24
10 6 10 26
10 8 0 18
10 8 2 20
10 8 4 22
10 8 6 24
10 8 8 26
10 8 10 28
10 10 0 20
10 10 2 22
10 10 4 24
10 10 6 26
10 10 8 28
10 10 10 30
.
.
.
Look at all 216 possible outcomes, 35 of them have a sum greater than 20.

Answer by Boreal(15235)   (Show Source): (Show Source):
You can put this solution on YOUR website! Look at cube 1
10
Draw a table
=0==2===4==6====8===10
0
2
4
6
8
10
If the first cube is 10, the second and third must sum to 12 or more. That is 2 and 10 in second row
4, and 8 or 10 in the third row; 6 and 6,8,10 in the fourth row; 8 and 4,6,8,10 in the fifth row, and 10 and 2,4,6,8,10 in the last row. There are 15 possibilities out of the 36 combinations or 15/36
Multiply that by 1/6 chance first is 10, and the probability is 15/216.
-------------------
Make the first cube 8 with 1/6 probability.
Now the pyramid of choices that work has shifted down so instead of 1,2,3,4,5 that work, it is 1,2,3,4 or 10 possibilities. The joint probability is 10/216
------------------
Make the first cube 6 with 1/6 probability and the rows that work have 1,2,3 choices or 6/36 probability. The joint probability is 6/216.
-----------------
Make the first cube 4 and there are only 1, 2 choices or 3/36 probability. That is 3/216 joint probability.
----------------
Make the first cube 2, and there is only one choice, 10 and 10 with 1/36 probability and 1/216 joint probability.
---------------
If the first cube is 0, there is no chance.
The joint probabilities sum to 15+10+6+3+1 , with denominator 216. The answer is 35/216.
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! Same answer, different way of counting.
There are  possible outcomes for each of the number cubes, possible outcomes for each of the number cubes,
so that makes  possible and equally probable outcomes. possible and equally probable outcomes.
If we can tell the number cubes apart
(for example because they are different colors, or because we roll them separately), we can tell apart those 216 outcomes.
We would count 10, 10, and 8 in the red, white, and blue cubes respectively as one outcome,
10, 8, and 10 in the red, white, and blue cubes respectively as another one of the 216 equally probable outcomes,
and 8, 10, and 10 in the red, white, and blue cubes respectively as yet another one.
Of course, if the 3 cubes are identical, and they are rolled together, we could not distinguish those 3 outcomes, and we would just see that getting one 8 and two 10's is 3 times more likely than getting three 10's.
There is only way for the numbers on all 3 cubes to be 10,
but there would be  ways to get two 10's and one 8, ways to get two 10's and one 8,
each way having the 8 appear on a different cube.
For a set of 3 different numbers, such as 10, 8 and 6,
there are  permutations that would give us that set of numbers. permutations that would give us that set of numbers.
That said, what sums of numbers would be greater than 20?
We have
 , ,  , ,
which can happen only one way each,
accounting for  of the of the 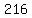 possible outcomes. possible outcomes.
There are also  sums greater than 20, that can happen sums greater than 20, that can happen  different ways: different ways:
 , ,
 , ,
 , ,
 , ,
 , ,
 , and , and
 . .
Those account for  of the of the 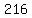 outcomes. outcomes.
Finally, there are  sums greater than 20, that can happen sums greater than 20, that can happen  different ways: different ways:
 , and , and  . .
Those sums account for  of the of the 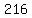 possible outcomes. possible outcomes.
All the other possible sums are equal or less than 20/.
The number of possible outcomes with a sum greater than 20 are
 of the of the 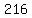 equally probable outcomes. equally probable outcomes.
so, the probability that the sum of the numbers rolled is greater than 20 is
 . .
numbers
Answer by MathTherapy(10552)   (Show Source): (Show Source):
You can put this solution on YOUR website! Three fair six-sided number cubes, each with faces labeled 0,2,4,6,8,10 are all rolled. What is the probability that the sum of the numbers rolled is greater than 20? Express your answer with a common fraction.
This is much easier than you might think.
Total number of events:  The numbers you're looking for are:
Doubles:
6, 8, 8
6, 6, 10
8, 8, 10
2, 10, 10
4, 10, 10
6, 10, 10
8, 10, 10
The numbers you're looking for are:
Doubles:
6, 8, 8
6, 6, 10
8, 8, 10
2, 10, 10
4, 10, 10
6, 10, 10
8, 10, 10 Number of ways ONE of these doubles appears in the 216 events: 
Now, since there are 7 DOUBLES, the number of ways those 7 doubles appear in the 216 events is: 7(3), or 21 times
Triplicates:
8, 8, 8
10, 10, 10
These triple numbers ONLY appear ONCE in the 216 events, and since there are 2 of them, then they appear in 2 of the 216 events
Distincts:
4, 8, 10
6, 8, 10
To find the number of times each of the above numbers appears in the 216 events, we calculate:  , and since there are 2 such sets, we get: 2(6), or 12 , and since there are 2 such sets, we get: 2(6), or 12
We now see that the number of numbers that appears with a sum > 20 is: 21 + 2 + 12.
So, the probability that the sum of the numbers rolled is greater than 20 = 
|
|
|