Question 1054920: I need the inverse of  with proof (like, f(f^-1(x)) that it's the inverse.
Found 2 solutions by Boreal, Theo:
Answer by Boreal(15235)   (Show Source):
You can put this solution on YOUR website! To find the inverse, change x and y
x=(3y-2)/(5y-3)
5xy-3x=3y-2
-3x=3y-2-5xy
-3x+2=y(3-5x)
y=(-3x+2)/(3-5x)
A line y=x splits the graphs.
Answer by Theo(13342)  (Show Source):
You can put this solution on YOUR website! let y = f(x).
your equation becomes y = (3x-2) / (5x-3)
replace y with x and x with y to get x = (3y-2) / (5y-3)
multiply both sides of the equation by (5y-3) to get x * (5y-3) = (3y-2)
simplify to get 5xy - 3x = 3y - 2
subtract 3y from both sides of the equation and add 3x to both sides of the equation to get 5xy - 3y = 3x - 2
factor out the y on the left hand side of the equation to get y * (5x - 3) = 3x - 2
divide both sides of the equaton by (5x - 3) to get y = (3x - 2) / (5x - 3).
your original equation was y = (3x - 2) / (5x - 3).
your inverse equation is y = (3x - 2) / (5x -3).
they're the same equation !!!!!.
is that possible?
if they are inverse equations of each other, then they will be reflections about the line y = x.
the following graph confirms that this relationship is true.
if they are inverse equations, then f(x,y) = g(y,x).
when x = 0, the value of y in the original equation becomes (3*0-2) / (5*0-3) which is equal to -2/-3 which is equal to 2/3.
when x = 2/3, the value of y in the inverse equation becomes (3*2/3 - 2) / (5*2/3 - 3) which becomes (2-2) / (10/3 - 3) which becomes 0 / (1/3) which is equal to 0.
therefore f(x,y) = 2/3 when x = 0 and g(y,x) becomes 0 when y = 2/3.
this confirms that the same equation is the inverse equation of itself.
the last test is fog(x) = c and gof(x) = x
f(x) = (3x-2)/(5x-3)
g(x) = (3x-2)/(5x-3)
fog(x) = f(g(x)) = f((3x-2)/(5x-3))
f((3x-2)/(5x-3)) is equal to (3*(3x-2)/(5x-3) -2) / (5*(3x-2)/(5x-3) - 3))
the following worksheet shows the details of the calculations.
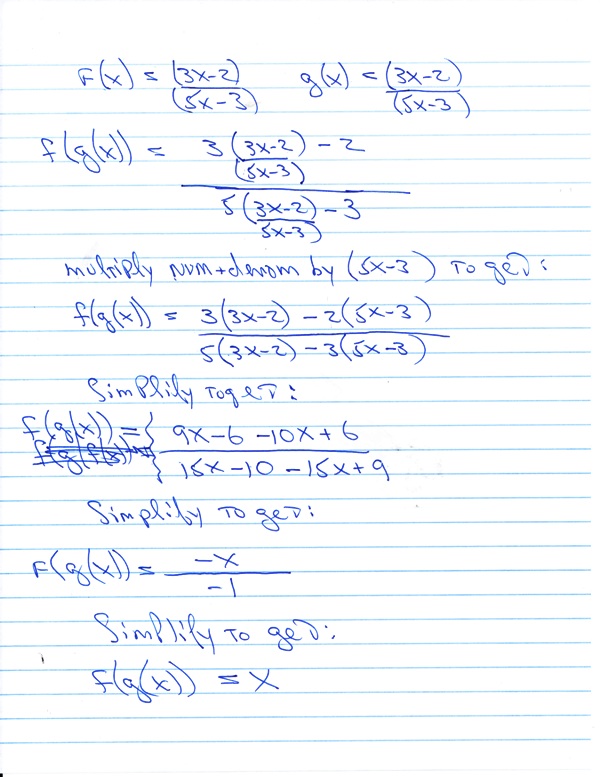
you wind up with f(g(x)) = x which passes the test for inverse functions.
if you did g(f(x)) you would have wound up with the same equation, so g(f(x)) is automatically equal to x also.
that's the final proof that f(x) and g(x) are inverse equations.
they are also identical equations.
|
|
|
