Question 618363: Given two parallel lines with a transversal, if one of the angles measure 50 degrees, find the measures of all the other angles. Explain how you found those angles.
Answer by KMST(5328)   (Show Source):
You can put this solution on YOUR website!  Angles 2, 4, 6, and 8 measure  , the other angles measure
THE REASONS (one of many ways to justify the conclusions):
I made the drawing so that the measure of angle 2 would be .
As for the other angles, we apply what was learned in geometry class:
Angles opposed "tip to tip", like the pair 2 and 4, and the pair 6 and 8, are called vertical and are congruent (same measure). So angle 4 measures because it is vertical to angle 2.
Angles in between the parallel lines, but on different sides of the transversal, like the pair of 4 and 6, are called alternate interior, and are also congruent. So angle 6 measures because it is alternate interior to angle 4.
And angle 8, vertical to 6, also measures .
Each of the other angles is supplementary to a angle, and must measure 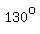 because a pair of supplementary angles must add to  .
NOTE:
There are different ways to explain the same conclusions. For example, you could say that angle 1 is suplementary to angle 2, or that it is supplementary to angle 4; it works one way or the other. You pick one, no need to say it both ways. Something similar happens for angles 3, 5, and 7.
|
|
|
