Question 272595: Can you help me solve the equation (2x^2-xy+y^2=8)and(xy=4). I have to find the value of x and y. I'm having trouble solving this particular problem. I just know the answer has to have 4 solutions. Thank you!
Answer by Theo(13342)   (Show Source):
You can put this solution on YOUR website! you have 2 equations that I presume must be solved simultaneously.
Those equations are:
(2x^2-xy+y^2=8)and(xy=4)
first thing you should be able to do is replace xy in the first equation with 4.
your first equation becomes:
2x^2 - 4 + y^2 = 8
add 4 to both sides of this equation to get:
2x^2 + y^2 = 8 + 4 which becomes:
2x^2 + y^2 = 12
since your second equation states that xy = 4, you can solve for y to get:
y = 4/x
replace y in your first equation with 4/x to get:
2x^2 + (4/x)^2 = 12
since (4/x)^2 = 4^2/x^2 = 16/x^2, your equation becomes:
2x^2 + 16/x^2 = 12
multiply both sides of this equation by x^2 to get:
2x^4 + 16 = 12x^2
subtract 12x^2 from both sides of this equation to get:
2x^4 - 12x^2 + 16 = 0
divide both sides of this equation by 2 to get:
x^4 - 6x^2 + 8 = 0
let k = x^2
your equation becomes:
k^2 - 6k + 8 = 0
factor this quadratic equation to get:
(k-2) * (k-4) = 0
since either one of these factors can be equal to 0 to make this equation true, then you have:
k-2 = 0 or k-4 = 0
solve for k to get:
k = 2 or k = 4
plugging those values into the quadratic equation will make that equation true.
the quadratic equation is k^2 - 6k + 8 = 0
when k = 2, this equation becomes 4 - 12 + 8 = 0 which is true.
when k = 4, this equation becomes 16 - 24 + 8 = 0 which is also true.
the values for k are both good.
since k = x^2 ( you set it that way), then you can solve for x to get:
x = +/- square root of k
when k = 4, x = +/- 2
when k = 2, x = +/- square root of 2.
we also know that y = 4/x
this means that:
when x = 2, y = 4/2 = 2
when x = -2, y = 4/(-2) = -2
square root of 2 is the same as 
when x = , y =  =  = 
when x =  , y =  =  =  = 
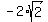
plug these values into your original equations and see whether those equations become true.
your original equations are:
(2x^2-xy+y^2=8)and(xy=4)
Since xy = 4, we changed the first equation to:
2x^2 - 4 + y^2 = 8
original equation is 2x^2 - 4 + y^2 = 8
when x = 2 and y = 2, this equation becomes:
2*2^2 - 4 + 2^2 = 8 which becomes:
2*4 - 4 + 4 = 8 which becomes:
8 - 4 + 4 = 8 which becomes:
8 = 8 which is true.
original equation is 2x^2 - 4 + y^2 = 8
when x = -2 and y = -2, this equation becomes:
2*(-2)^2 - 4 + (-2)^2 = 8 which becomes:
2*4 - 4 + 4 = 8 which becomes:
8 - 4 + 4 = 8 which becomes:
8 = 8 which is true.
original equation is 2x^2 - 4 + y^2 = 8
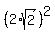when x = and y = , this equation becomes:
 +  = 8 which becomes:
2*2 - 4 + 4*2 = 8 which becomes:
4 - 4 + 8 = 8 which becomes:
8 = 8 which is true.
original equation is 2x^2 - 4 + y^2 = 8
when x = and y = 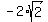, this equation becomes:
 +  = 8 which becomes:
2*2 - 4 + 4*2 = 8 which becomes:
4 - 4 + 8 = 8 which becomes:
8 = 8 which is true.
your second equation is xy = 4
when x = 2 and y = 2, this equation becomes 4 = 4 which is true.
when x = -2 and y = -2, this equation becomes 4 = 4 which is true.
when x = and y = , this equation becomes:
 = 4 which becomes:
2*2 = 4 which becomes:
4 = 4 which is true.
when x = and y = 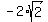, this equation becomes:
 = 4 which becomes:
2 * 2 = 4 which becomes
4 = 4 which is true.
All equations are true so these values are good.
they are:
when x = 2, y = 2
when x = -2, y = -2
when x = , y =
when x = , y =
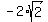
those are your 4 "sets" of answers.
each answer is a pair of values, 1 for x and 1 for y.
|
|
|
