Question 107512: I am trying to help my daughter with her homework, but since I have no idea what I am doing I hope that having the answer will help me out:
Cricket Problem: Based on information in Deep River Jim's Wilderness Trailbook, the rate at which crickets chirp is a lenear function of temperature. At 55 degrees F they make 70 chirps per minute and at 69 degrees F they make 126 chirps per minute.
a) Write the equation expressing chirping rate as a function of temperature.
b) Predict the chirping rate at 90 degrees F.
c) How warm is it if they are chirping 120 chirps per minute?
d) Calculate the temperature-intercept. What does this tell you about this numbeer in the real-world?
e) Calculate the chirping-intercept. What does the chirping-intercept tell you about the real-worl?
f) Shetch and label the graph.
Thank you for any help.
Brian
Found 3 solutions by stanbon, Fombitz, solver91311:
Answer by stanbon(75887)   (Show Source):
You can put this solution on YOUR website! Cricket Problem: Based on information in Deep River Jim's Wilderness Trailbook, the rate at which crickets chirp is a lenear function of temperature. At 55 degrees F they make 70 chirps per minute and at 69 degrees F they make 126 chirps per minute.
-----------
You have two points: (55,70) and (69,126)
a) Write the equation expressing chirping rate as a function of temperature.
slope = [126-70]/[69-55] = 56/14 = 4
chirps = slope(temp) + b
Substitute chirps=70,temp=55,slope=4 to solve for "b":
70 = 4(55)+b
b = -150
EQUATION: chirps = 4(temp)-150
--------------------------
b) Predict the chirping rate at 90 degrees F.
chirps = 4*90-150
chirps = 360-150
chirps = 210
------------------------------
c) How warm is it if they are chirping 120 chirps per minute?
120 = 4*temp - 150
270 = 4*temp
temp = 135/2 = 67.5 degrees
--------------------
d) Calculate the temperature-intercept. What does this tell you about this number in the real-world?
temp-intercept = -150
It is unrealistic as it occurs when the termperature is zero.
Of course there are no crickets around when the temp is zero.
-------------------
e) Calculate the chirping-intercept. What does the chirping-intercept tell you about the real-world?
nothing
------------------
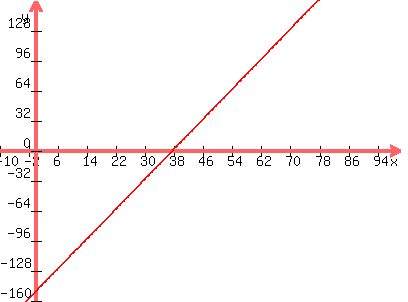
f) Shetch and label the graph.
Plot the two points and draw a line thru them.
---------
Cheers,
Stan H.
Answer by Fombitz(32388)  (Show Source):
Answer by solver91311(24713)  (Show Source):
You can put this solution on YOUR website! The first part of this problem involves using two points to define a straight-line (linear) relationship. Since we are given the two points in the problem statement, let's begin with the two-point form of a linear equation:
The next step is to decide which axis will represent which parameter, i.e. chirps or temperature. Since the problem asks for an expression of chirps per minute as a function of temperature, we need to make y represent the chirping rate and x represent the temperature. That is because the standard way to represent something that is a function of another thing is to make the 'something' be the y or vertical axis value, and the 'another thing' be the x or horizontal axis value.
Now we need to express our points in terms of ordered pairs, (x1,y1)and (x2,y2). The first data point says 70 chirps at 55 degrees, so:
(x1,y1)=(55, 70)
Similarly,
(x2,y2)=(69, 126).
Now that we have x1, x2, y1, and y2 identified, we can put these values into the two-point form of the line, thus:
Next we do a little arithmetic to simplify things:
 (apply the distributive property)
 (add 70 to both sides)
That concludes Part a).
Part b) wants us to predict the number of chirps at 90 degrees. Since x stands for temperature, just substitute 90 for x in the equation we just developed and do the arithmetic.
 chirps per minute.
Part c) wants to know the temperature if you can count 120 chirps per minute.
Use the same equation, except this time, substitute 120 for the y value:
 (add 150 to both sides)
 (divide both sides by 4)
And the answer is 67.5 degrees.
Part d) wants us to calculate the temperature intercept, that is to say what is the value of x (temperature) when y (chirp rate) is zero.
 (add 150 to both sides)
So the chirps stop altogether when the temperature drops to 37.5 degrees, to put it into real-world terms.
Part e) asks for the chirp intercept. This is just the opposite of part d), i.e. what is the value of y (chirp rate) when x (temperature) is zero.
This means that the cricket will chirp MINUS 150 times per minute when the temperature is zero. Of course, this is absurd. In fact, what we have demonstrated is that the function we have defined, namely , has a defined region of linearity in which we can use the function to predict the number of chirps per minute based on the temperature. We discovered the lower limit of this region in Part d), and presumably there is an upper limit temperature at which crickets would spontaneously combust causing them to stop chirping.
Part f)
I'm going to give you a graph, but this system doesn't give me the capability to label it, so you will have to figure that part out for yourself.
The vertical axis is the y axis, or number of chirps per minute, while the horizontal axis is the x axis, or temperature in this case. The points forming the slanted line represent our function. Note that the function crosses the x-axis at about 37.5 on the scale. That is the temperature or x-intercept. Also note that the line crosses the y axis at about -150, but as we discussed, the function isn't valid as illustrated for any temperature less than 37.5 degrees.
Hope this helps.
|
|
|
