SOLUTION: Find the area of the region enclosed by the graph of x^2 + y^2 = 2x - 6y + 6.

Algebra ->  Coordinate-system -> SOLUTION: Find the area of the region enclosed by the graph of x^2 + y^2 = 2x - 6y + 6.      Log On


   

Question 1209278: Find the area of the region enclosed by the graph of x^2 + y^2 = 2x - 6y + 6.
Answer by ikleyn(52799) About Me  (Show Source):
You can put this solution on YOUR website!
.
Find the area of the region enclosed by the graph of x^2 + y^2 = 2x - 6y + 6.
~~~~~~~~~~~~~~~~~ 

Write the given equation in the standard form of the ellipse/circle equation

    x^2 + y^2 = 2x - 6y + 6,

    x^2 -2x + y^2 + 6x = 6,

    (x^2 - 2x + 1) + (y^2 + 6x + 9) = 6 + 1 + 9,

    (x-1)^2 + (y+3)^2 = 16.


This equation represents a circle of the radius  r = 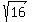sqrt%2816%29 = 4.  centered at point (1,-3).


The area of this circle is  

    pi%2Ar%5E2  = 16%2Api = 16*3.14159265 = 50.2654824 square units (approximately).    ANSWER

Solved.